Ellipse by Conical Section
This post examines elliptical sections which are created by taking a diagonal cutting plane through a right cone.
When the cutting plane goes through the cone at an angle, the surface created takes the form of an ellipse:
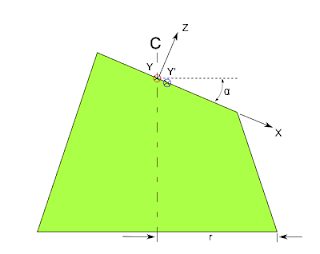
To verify this statement, let's look at the cone from the side and affix the origin of an x-y-z coordinate system to the center line of the cone. Positive x is on the cutting plane, aligned with the long side of the cut. Positive y is on the cutting plane, aligned with the short side of the cut and going into the page. Positive z is perpendicular to the cutting plane. α is the angle at which the cutting plane cut through the cone, with respect to the horizontal. See the following image for an illustration of these properties.
Looking at the section from above, and perpendicular to, the plane of the section, it appears as illustrated in the following image (the z-axis is coming out of the page, straight at the viewer):
One feature of this section should be noted: the center of the ellipse does not coincide with the center line of the cone that produced it. The center line of the cone intersects the elliptical plane at the origin of the X-Y-Z coordinate system. HOWEVER, the center of the ellipse is at the origin of the Xe-Ye-Ze coordinate system, which is offset by an amount ro from the origin of the X-Y-Z system in the positive X direction (see the image above).
Numbers will now be assigned to the section, and some numerical results calculated, to confirm that an ellipse is, indeed, described.
Values for a and e will be the same as were used in the previous post (for a section created through a cylinder):
a = 1
e = 0.786151377746
An infinite number of cone and cutting plane combinations could produce an ellipse with this eccentricity, so one more constraining parameter, gamma, will be defined:
γ = h/r
where h is the height of the cone, and
r is the radius of the bottom of the cone.
γ now serves as a parameter to define a cone uniquely by its height/radius ratio. Then
α = arcsin[(γ e)/√(γ² + 1)] and
ro = a (tan(α)/γ)
For the purpose of the following numerical example, γ = 1.27201964953.
The necessary cutting plane is then α = 0.666239432494 radians, and
ro = 0.618033988735.
To summarize:
γ = 1.27201964953
α = 0.666239432494 radians
e = 0.786151377746
a = 1
ro = 0.618033988735
b = √(1 - e²) = 0.618033988764
(Note that the angle of the cutting plane, α, is much smaller in this case than it was when a section was taken through a cylinder--to produce an ellipse of the same eccentricity.)
Now to compute some data points. Keep in mind that xe and ye are in the plane of the ellipse.
Start with a value of xe in the Xe-Ye plane.
Calculate the ye value at this xe point.
Projecting xe into the horizontal plane and measuring with respect to the cone axis,
x = (ro + xe) cos(α)
The radius of the cone at this level is
r = (γ cos(α) + sin(α) xe)/γ
On a circle in the horizontal plane, this x value corresponds to an angle of
θ = arccos(x/r)
In turn, this angle corresponds to a ye value:
ye = r sin(θ)
As a quick check, at xe = 0,
r = cos(α) = 0.786151377757
θ = arccos(tan(α)/γ) = arccos(0.618033988754) = 0.904556894297
Then ye = r sin(θ) = 0.786151377757*sin(0.904556894297) = 0.618033988738
Remember that this value of ye corresponds to b, the mid-point of the ellipse. And because this value is the same as the one calculated from the standard equation for an ellipse, b = √(1 - e²), this is a good indication that the section is an ellipse.
An alternative to this rather roundabout way is to use the following equation for ye:
Whichever technique is used, computing some values for ye,
for xe = 0.05, ye = 0.617260962835
for xe = 0.10, ye = 0.614936054525
and so on.
Values for a quarter-section of the ellipse are tabulated in another blog post:
Blog Post: Ellipse Sample Datapoints
Datapoints computed from the expression for ye above are tabulated in the column under the heading ye. Note that these values are the same as the values computed from the standard equation of an ellipse.
Apparently, taking a diagonal cutting plane through a right cone does, indeed, produce an ellipse.
When the cutting plane goes through the cone at an angle, the surface created takes the form of an ellipse:
To verify this statement, let's look at the cone from the side and affix the origin of an x-y-z coordinate system to the center line of the cone. Positive x is on the cutting plane, aligned with the long side of the cut. Positive y is on the cutting plane, aligned with the short side of the cut and going into the page. Positive z is perpendicular to the cutting plane. α is the angle at which the cutting plane cut through the cone, with respect to the horizontal. See the following image for an illustration of these properties.
Looking at the section from above, and perpendicular to, the plane of the section, it appears as illustrated in the following image (the z-axis is coming out of the page, straight at the viewer):
One feature of this section should be noted: the center of the ellipse does not coincide with the center line of the cone that produced it. The center line of the cone intersects the elliptical plane at the origin of the X-Y-Z coordinate system. HOWEVER, the center of the ellipse is at the origin of the Xe-Ye-Ze coordinate system, which is offset by an amount ro from the origin of the X-Y-Z system in the positive X direction (see the image above).
Numbers will now be assigned to the section, and some numerical results calculated, to confirm that an ellipse is, indeed, described.
Values for a and e will be the same as were used in the previous post (for a section created through a cylinder):
a = 1
e = 0.786151377746
An infinite number of cone and cutting plane combinations could produce an ellipse with this eccentricity, so one more constraining parameter, gamma, will be defined:
γ = h/r
where h is the height of the cone, and
r is the radius of the bottom of the cone.
γ now serves as a parameter to define a cone uniquely by its height/radius ratio. Then
α = arcsin[(γ e)/√(γ² + 1)] and
ro = a (tan(α)/γ)
For the purpose of the following numerical example, γ = 1.27201964953.
The necessary cutting plane is then α = 0.666239432494 radians, and
ro = 0.618033988735.
To summarize:
γ = 1.27201964953
α = 0.666239432494 radians
e = 0.786151377746
a = 1
ro = 0.618033988735
b = √(1 - e²) = 0.618033988764
(Note that the angle of the cutting plane, α, is much smaller in this case than it was when a section was taken through a cylinder--to produce an ellipse of the same eccentricity.)
Now to compute some data points. Keep in mind that xe and ye are in the plane of the ellipse.
Start with a value of xe in the Xe-Ye plane.
Calculate the ye value at this xe point.
Projecting xe into the horizontal plane and measuring with respect to the cone axis,
x = (ro + xe) cos(α)
The radius of the cone at this level is
r = (γ cos(α) + sin(α) xe)/γ
On a circle in the horizontal plane, this x value corresponds to an angle of
θ = arccos(x/r)
In turn, this angle corresponds to a ye value:
ye = r sin(θ)
As a quick check, at xe = 0,
r = cos(α) = 0.786151377757
θ = arccos(tan(α)/γ) = arccos(0.618033988754) = 0.904556894297
Then ye = r sin(θ) = 0.786151377757*sin(0.904556894297) = 0.618033988738
Remember that this value of ye corresponds to b, the mid-point of the ellipse. And because this value is the same as the one calculated from the standard equation for an ellipse, b = √(1 - e²), this is a good indication that the section is an ellipse.
An alternative to this rather roundabout way is to use the following equation for ye:
Whichever technique is used, computing some values for ye,
for xe = 0.05, ye = 0.617260962835
for xe = 0.10, ye = 0.614936054525
and so on.
Values for a quarter-section of the ellipse are tabulated in another blog post:
Blog Post: Ellipse Sample Datapoints
Datapoints computed from the expression for ye above are tabulated in the column under the heading ye. Note that these values are the same as the values computed from the standard equation of an ellipse.
Apparently, taking a diagonal cutting plane through a right cone does, indeed, produce an ellipse.
Labels: conical section, ellipse, elliptical section